4. 集合と関数
集合,関係,関数の用語は,数学の全分野における各概念の構成のための統一的な言語を提供します.関数と関係は集合で定義できるので,数学の基礎として公理的集合論を利用することができます.
Leanは集合の代わりに 型 という原始的な概念を基礎にしており,型の間には関数を定義することができます.Leanではすべての式が型を持ちます: 例えば自然数,実数,実数から実数への関数,群,ベクトル空間などはすべて型です.式の中には型 そのもの であるものもあり,それらの型は Type です.LeanとMathlibは新しい型や,それらの型のオブジェクトを定義する方法を提供しています.
概念的には,型はオブジェクトの単なる集まりと考えることができます.すべてのオブジェクトに型を要求することには複数の利点があります.例えば, + のような記法をオーバーロードできるようになり,またLeanがオブジェクトの型から多くの情報を推測できるようになり,入力をより簡潔にすることができます.また,型システムによって,関数に渡す引数の数を間違えたり,関数の引数の型を間違えた場合にLeanにエラーとして教えてもらうことができるようになります.
Leanのライブラリは初等的な集合論の概念を定義しています.集合論とは対照的に,Leanでは集合は常にある型のオブジェクトの集まりです.例えば自然数の集合や実数から実数への関数の集合などです.型と集合の違いを飲み込むには慣れが必要ですが,この章ではその要点を説明します.
4.1. 集合
α が型であるとき, Set α 型は α の要素からなる集合の集まりです.この型は通常の集合論的な操作や関係をサポートしています.例えば s ⊆ t は s が t の部分集合であること, s ∩ t は s と t の共通部分, s ∪ t は s と t の合併を表します.部分集合の関係は \ss か \sub で,共通部分は \i もしくは \cap ,合併は \un か \cup で入力できます.またMathlibは univ という集合も定義しています.これは α のすべての要素からなる集合です.そして \empty で入力される空集合 ∅ も定義しています. x : α と s : Set α が与えられた時,式 x ∈ s は x が s のメンバーであることを表します.集合の帰属関係に言及する定理は,しばしばその名前に mem を含みます.式 x ∉ s は ¬ x ∈ s を省略したものです. ∈ は \in か \mem で, ∉ は \notin で入力できます.
集合について証明する一つの方法は, rw や simp を使って定義を展開することです.以下の2つ目の例では, simp only を使うことで simp がLean内部にある等式についてのデータベース全体ではなく,指定した等式のリストだけを使うようにしています. rw とは異なり, simp は全称量化子や存在量化子の中でも単純化を行うことができます.以下の証明を一行ずつたどれば,これらのタクティクの効果を見ることができます.
variable {α : Type*}
variable (s t u : Set α)
open Set
example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u := by
rw [subset_def, inter_def, inter_def]
rw [subset_def] at h
simp only [mem_setOf]
rintro x ⟨xs, xu⟩
exact ⟨h _ xs, xu⟩
example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u := by
simp only [subset_def, mem_inter_iff] at *
rintro x ⟨xs, xu⟩
exact ⟨h _ xs, xu⟩
この例では,定理の短い名前にアクセスするために Set 名前空間を開いています.しかし,実は rw と simp の呼び出しは削除することができます.
example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u := by
intro x xsu
exact ⟨h xsu.1, xsu.2⟩
ここで行われたことは 定義に基づく簡約 (definitional reduction)として知られるもので, intro コマンドとその後の無名コンストラクタの意味が通るようにLeanが定義を自動で展開しています.下記の例でも同じ現象が発生しています:
example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u :=
fun x ⟨xs, xu⟩ ↦ ⟨h xs, xu⟩
合併を扱うには, Set.union_def と Set.mem_union を使うことができます. x ∈ s ∪ t は x ∈ s ∨ x ∈ t に展開されるため, cases タクティクを使って強制的に定義に基づく簡約を行うこともできます.
example : s ∩ (t ∪ u) ⊆ s ∩ t ∪ s ∩ u := by
intro x hx
have xs : x ∈ s := hx.1
have xtu : x ∈ t ∪ u := hx.2
rcases xtu with xt | xu
· left
show x ∈ s ∩ t
exact ⟨xs, xt⟩
· right
show x ∈ s ∩ u
exact ⟨xs, xu⟩
共通部分は合併よりも強く結合するため, (s ∩ t) ∪ (s ∩ u) という式に括弧を使う必要はありませんが,括弧を使うことで式の意味がより明確になります.以下は同じ事実のより短い証明です:
example : s ∩ (t ∪ u) ⊆ s ∩ t ∪ s ∩ u := by
rintro x ⟨xs, xt | xu⟩
· left; exact ⟨xs, xt⟩
· right; exact ⟨xs, xu⟩
演習問題として,もう一方の包含を証明してみましょう:
example : s ∩ t ∪ s ∩ u ⊆ s ∩ (t ∪ u) := by
sorry
rintro を使う時,パースが正しく行われるように,選言のパターン h1 | h2 を括弧で囲む必要があることを知っておくと良いでしょう.
Mathlibでは s \ t で表される差集合も定義されています.ここでバックスラッシュは \\ で入力される特別なUnicode文字です.式 x ∈ s \ t は x ∈ s ∧ x ∉ t に展開されます.( ∉ は \notin で入力できます.)この定義は Set.diff_eq や dsimp や Set.mem_diff を使って手動で展開することもできますが,使わないこともできます.以下の包含関係に関する命題では,これを避ける方法で2通りの証明を示します.
example : (s \ t) \ u ⊆ s \ (t ∪ u) := by
intro x xstu
have xs : x ∈ s := xstu.1.1
have xnt : x ∉ t := xstu.1.2
have xnu : x ∉ u := xstu.2
constructor
· exact xs
intro xtu
-- x ∈ t ∨ x ∈ u
rcases xtu with xt | xu
· show False; exact xnt xt
· show False; exact xnu xu
example : (s \ t) \ u ⊆ s \ (t ∪ u) := by
rintro x ⟨⟨xs, xnt⟩, xnu⟩
use xs
rintro (xt | xu) <;> contradiction
演習問題として,反対向きの包含を証明してみましょう:
example : s \ (t ∪ u) ⊆ (s \ t) \ u := by
sorry
2つの集合が等しいことを証明するには,一方の集合のすべての要素がもう片方の集合の要素であることを示せば十分です.この原理は「外延性(extensionality)」として知られており,名前としてはそのまま ext タクティクでこれを扱うことができます.
example : s ∩ t = t ∩ s := by
ext x
simp only [mem_inter_iff]
constructor
· rintro ⟨xs, xt⟩; exact ⟨xt, xs⟩
· rintro ⟨xt, xs⟩; exact ⟨xs, xt⟩
繰り返しになりますが, simp only [mem_inter_iff] の行を削除しても証明には影響しません.実際,証明項による難解な証明で構わなければ,次のように1行で証明できます:
example : s ∩ t = t ∩ s :=
Set.ext fun x ↦ ⟨fun ⟨xs, xt⟩ ↦ ⟨xt, xs⟩, fun ⟨xt, xs⟩ ↦ ⟨xs, xt⟩⟩
以下は simp を使ったさらに短い証明です:
example : s ∩ t = t ∩ s := by ext x; simp [and_comm]
ext の代わりに s ⊆ t と t ⊆ s の証明から集合間の等式 s = t を導出する定理 Subset.antisymm を使うことができます.
example : s ∩ t = t ∩ s := by
apply Subset.antisymm
· rintro x ⟨xs, xt⟩; exact ⟨xt, xs⟩
· rintro x ⟨xt, xs⟩; exact ⟨xs, xt⟩
これの証明項バージョンを完成させてみましょう:
example : s ∩ t = t ∩ s :=
Subset.antisymm sorry sorry
上記で sorry をアンダースコアで書き換えてその上にカーソルを置くと,Leanがその時点で何を期待しているかが表示されることを覚えておいてください.
以下の集合論的な等式の証明は楽しいかもしれません:
example : s ∩ (s ∪ t) = s := by
sorry
example : s ∪ s ∩ t = s := by
sorry
example : s \ t ∪ t = s ∪ t := by
sorry
example : s \ t ∪ t \ s = (s ∪ t) \ (s ∩ t) := by
sorry
Leanで集合を表現するとき,その裏で何が行われているのか説明しましょう.型理論において,ある型 α の 性質 (property)や 述語 (predicate)は単なる関数 P : α → Prop です.これは理にかなっています: a : α が与えられた時, P a はまさに a に対して P が成り立っているという命題に他ならないからです.Mathlibでは Set α は α → Prop と定義され, x ∈ s は s x と定義されます.言い換えれば,集合は性質であり,対象として扱われます.
ライブラリでは集合の内包表記も定義しています.式 { y | P y } は (fun y ↦ P y) に展開されます.したがって, x ∈ { y | P y } は P x に簡約されます.これを用いて偶数であるという性質を偶数の集合に変えることができます:
def evens : Set ℕ :=
{ n | Even n }
def odds : Set ℕ :=
{ n | ¬Even n }
example : evens ∪ odds = univ := by
rw [evens, odds]
ext n
simp [-Nat.not_even_iff_odd]
apply Classical.em
この証明を順を追って見て,何が起こっているのか理解してください.ここでゴールにある ¬ Even n を保持するために,単純化器に Nat.not_even_iff を 使わない よう指示していることに注意してください.そして rw [evens, odds] の行を削除しても証明がまだ機能することを確認してください.
実際,内包表記は以下を定義する際に用いられています.
s ∩ tは{x | x ∈ s ∧ x ∈ t}で定義されます.s ∪ tは{x | x ∈ s ∨ x ∈ t}で定義されます.∅は{x | False}で定義されます.univは{x | True}で定義されます.
∅ と univ についてはどの型についてのものなのかをLeanが正しく推論できないため,明示的に型を示す必要があります.以下の例では,Leanが必要に応じて最後の2つの定義をどのように展開するかを示しています.2つ目の例で用いられている trivial はライブラリにおいて True の標準的な証明です.
example (x : ℕ) (h : x ∈ (∅ : Set ℕ)) : False :=
h
example (x : ℕ) : x ∈ (univ : Set ℕ) :=
trivial
演習問題として,以下の包含を証明しましょう.その際にはまず intro n を使って部分集合の定義を展開し,そして単純化を使って集合論的な構成を論理に落とし込みます.また定理 Nat.Prime.eq_two_or_odd と Nat.odd_iff を使うことをお勧めします.
example : { n | Nat.Prime n } ∩ { n | n > 2 } ⊆ { n | ¬Even n } := by
sorry
注意:少し混乱するかもしれませんが,Mathlibでは Prime という述語に複数のバージョンがあります.最も一般的な定義では,零要素を持つ任意の可換モノイドで使うことができます.これに対し Nat.Prime は自然数専用の述語です.幸いなことに,特定のケースではこの2つの概念が一致するという定理があるため,いつでも一方を他方に書き換えることができます.
#print Prime
#print Nat.Prime
example (n : ℕ) : Prime n ↔ Nat.Prime n :=
Nat.prime_iff.symm
example (n : ℕ) (h : Prime n) : Nat.Prime n := by
rw [Nat.prime_iff]
exact h
rwa タクティクは rw に続いて assumption タクティクを実行します.
example (n : ℕ) (h : Prime n) : Nat.Prime n := by
rwa [Nat.prime_iff]
Leanでは「 s のすべての要素 x について,」を意味する ∀ x, x ∈ s → ... の省略形として ∀ x ∈ s, ... という記法を使用できます.またこれと同じように「 s の要素である x が存在し,」に対する ∃ x ∈ s, ..., という記法も使用できます.これらは 束縛量化子 (bounded quantifiers)と呼ばれることがあります.これはこの構文が変数の範囲を集合 s に限定する役割を果たすからです.このため,これらの記法を用いるライブラリ中の定理の名前にはしばしば ball や bex が含まれます. ∃ x ∈ s, ... が ∃ x, x ∈ s ∧ ..., と等価であることは定理 bex_def で主張されていますが,この定理を用いずとも rintro と use ,そして無名コンストラクタを用いることでこの2つの差異をほぼ無視できます.そのため通常 bex_def を使って明示的に変換する必要はありません.以下は上記の記法の使用例です:
variable (s t : Set ℕ)
example (h₀ : ∀ x ∈ s, ¬Even x) (h₁ : ∀ x ∈ s, Prime x) : ∀ x ∈ s, ¬Even x ∧ Prime x := by
intro x xs
constructor
· apply h₀ x xs
apply h₁ x xs
example (h : ∃ x ∈ s, ¬Even x ∧ Prime x) : ∃ x ∈ s, Prime x := by
rcases h with ⟨x, xs, _, prime_x⟩
use x, xs
これらの少し異なったバージョンを証明してみましょう:
section
variable (ssubt : s ⊆ t)
example (h₀ : ∀ x ∈ t, ¬Even x) (h₁ : ∀ x ∈ t, Prime x) : ∀ x ∈ s, ¬Even x ∧ Prime x := by
sorry
example (h : ∃ x ∈ s, ¬Even x ∧ Prime x) : ∃ x ∈ t, Prime x := by
sorry
end
添字付き集合族の合併と共通部分も集合論では重要な構成です.\(A_0, A_1, A_2, \ldots\) で表される α の部分集合の族は,関数 A : ℕ → Set α でモデル化することができます.ここで ⋃ i, A i は集合族の合併を, ⋂ i, A i は集合族の共通部分を表します.ここで添字に用いられている i の型として自然数を用いていますが特段自然数の性質を用いているわけではないため, ℕ は任意の型 I で置き換えることができます.以下にこれらの使い方を示します.
variable {α I : Type*}
variable (A B : I → Set α)
variable (s : Set α)
open Set
example : (s ∩ ⋃ i, A i) = ⋃ i, A i ∩ s := by
ext x
simp only [mem_inter_iff, mem_iUnion]
constructor
· rintro ⟨xs, ⟨i, xAi⟩⟩
exact ⟨i, xAi, xs⟩
rintro ⟨i, xAi, xs⟩
exact ⟨xs, ⟨i, xAi⟩⟩
example : (⋂ i, A i ∩ B i) = (⋂ i, A i) ∩ ⋂ i, B i := by
ext x
simp only [mem_inter_iff, mem_iInter]
constructor
· intro h
constructor
· intro i
exact (h i).1
intro i
exact (h i).2
rintro ⟨h1, h2⟩ i
constructor
· exact h1 i
exact h2 i
添字付き集合族の合併や共通部分の表記ではしばしば括弧を使う必要があります.これは量化子の場合と同様に,Leanが束縛された変数のスコープを可能な限り広げようとするからです.
次の等式を証明してみましょう.この証明は2方向の包含関係を示すことで行いますが,片方は古典論理が必要となります!適切なところで by_cases xs : x ∈ s を使うと良いでしょう.
example : (s ∪ ⋂ i, A i) = ⋂ i, A i ∪ s := by
sorry
またMathlibは束縛された量化子に似た束縛された合併と共通集合を持っています.これらは mem_iUnion₂ と mem_iInter₂ で定義に展開することができます.以下の例で示すように,Leanの simp タクティクはこれらの置換も行ってくれます.
def primes : Set ℕ :=
{ x | Nat.Prime x }
example : (⋃ p ∈ primes, { x | p ^ 2 ∣ x }) = { x | ∃ p ∈ primes, p ^ 2 ∣ x } :=by
ext
rw [mem_iUnion₂]
simp
example : (⋃ p ∈ primes, { x | p ^ 2 ∣ x }) = { x | ∃ p ∈ primes, p ^ 2 ∣ x } := by
ext
simp
example : (⋂ p ∈ primes, { x | ¬p ∣ x }) ⊆ { x | x = 1 } := by
intro x
contrapose!
simp
apply Nat.exists_prime_and_dvd
上記と似た次の例題を解いてみましょう.ここで eq_univ と入力し始めると,タブの補完が apply eq_univ_of_forall をまず使うことを教えてくれるでしょう.また Nat.exists_infinite_primes という定理を使うこともお勧めします.
example : (⋃ p ∈ primes, { x | x ≤ p }) = univ := by
sorry
集合の集まり s : Set (Set α) について,これらの合併 ⋃₀ s は型 Set α を持ち, {x | ∃ t ∈ s, x ∈ t} と定義されます.同様に共通部分 ⋂₀ s は {x | ∀ t ∈ s, x ∈ t} で定義されます.これらの演算子はそれぞれ sUnion と sInter と呼ばれます.以下の例では束縛された合併と共通部分との関係を示します.
variable {α : Type*} (s : Set (Set α))
example : ⋃₀ s = ⋃ t ∈ s, t := by
ext x
rw [mem_iUnion₂]
simp
example : ⋂₀ s = ⋂ t ∈ s, t := by
ext x
rw [mem_iInter₂]
rfl
Mathlibでは,これらの等式は sUnion_eq_biUnion と sInter_eq_biInter と呼ばれています.
4.2. 関数
f : α → β が関数で p が β 型の項の集合であるとします.このとき p の f による逆像を考えることができますが,これはMathlibでは preimage f p と呼ばれ,{x | f x ∈ p} として定義され,f ⁻¹' p と表記されます.式 x ∈ f ⁻¹' p は f x ∈ p に簡約されます.次の例のようにこれはしばしば便利です:
variable {α β : Type*}
variable (f : α → β)
variable (s t : Set α)
variable (u v : Set β)
open Function
open Set
example : f ⁻¹' (u ∩ v) = f ⁻¹' u ∩ f ⁻¹' v := by
ext
rfl
また s が α 型の集合であるとします.このとき s の f による像が考えられますが,これはMathlibでは image f s と呼ばれ,{y | ∃ x, x ∈ s ∧ f x = y} で定義され,f '' s と表記されます.よって仮定 y ∈ f '' s は ⟨x, xs, xeq⟩ という3つ組に分解できます.これは x : α が仮定 xs : x ∈ s と xeq : f x = y を満たすことを意味しています. rintro タクティク内で用いられている rfl タグ( Section 3.2 参照)はまさにこのような状況のために設計されています.
example : f '' (s ∪ t) = f '' s ∪ f '' t := by
ext y; constructor
· rintro ⟨x, xs | xt, rfl⟩
· left
use x, xs
right
use x, xt
rintro (⟨x, xs, rfl⟩ | ⟨x, xt, rfl⟩)
· use x, Or.inl xs
use x, Or.inr xt
また use タクティクを使うと, rfl を適用することでゴールに近づけることができる場合には rfl を適用してくれることにも注意してください.
ここで別の例を見てみましょう.
example : s ⊆ f ⁻¹' (f '' s) := by
intro x xs
show f x ∈ f '' s
use x, xs
use x, xs という行は,まさに f x ∈ f '' s を示すための専用の定理 mem_image_of_mem f xs で置き換えることもできます.しかし,像が存在量化子で定義されていることを知っていると何かと便利なことが多いものです.
次の同値を示すことは良い演習問題になるでしょう.
example : f '' s ⊆ v ↔ s ⊆ f ⁻¹' v := by
sorry
この命題は image f と preimage f が一種の ガロア接続 (Galois connection) [1] であることを主張しています.ここではベキ集合 Set α と Set β が部分集合の包含関係に関して半順序集合になっています.Mathlibでは,この同値性は image_subset_iff と名付けられています.実際に使う場合には右辺がより便利な表現であることが多いです.なぜなら, y ∈ f ⁻¹' t は f y ∈ t に展開されるのに対し, x ∈ f '' s を扱うには存在量化子を分解する必要があるからです.
読者に楽しんでいただくため,ここに集合についての等式をたくさん用意しました.これらすべてを一度にやる必要はありません.いくつかやったら,残りは雨の日のためにとっておきましょう.
example (h : Injective f) : f ⁻¹' (f '' s) ⊆ s := by
sorry
example : f '' (f ⁻¹' u) ⊆ u := by
sorry
example (h : Surjective f) : u ⊆ f '' (f ⁻¹' u) := by
sorry
example (h : s ⊆ t) : f '' s ⊆ f '' t := by
sorry
example (h : u ⊆ v) : f ⁻¹' u ⊆ f ⁻¹' v := by
sorry
example : f ⁻¹' (u ∪ v) = f ⁻¹' u ∪ f ⁻¹' v := by
sorry
example : f '' (s ∩ t) ⊆ f '' s ∩ f '' t := by
sorry
example (h : Injective f) : f '' s ∩ f '' t ⊆ f '' (s ∩ t) := by
sorry
example : f '' s \ f '' t ⊆ f '' (s \ t) := by
sorry
example : f ⁻¹' u \ f ⁻¹' v ⊆ f ⁻¹' (u \ v) := by
sorry
example : f '' s ∩ v = f '' (s ∩ f ⁻¹' v) := by
sorry
example : f '' (s ∩ f ⁻¹' u) ⊆ f '' s ∩ u := by
sorry
example : s ∩ f ⁻¹' u ⊆ f ⁻¹' (f '' s ∩ u) := by
sorry
example : s ∪ f ⁻¹' u ⊆ f ⁻¹' (f '' s ∪ u) := by
sorry
また,次に挙げる集合族の合併と共通部分に関する像と逆像の挙動についての演習問題に挑戦するのもよいでしょう.3番目の演習問題では,添字集合が空でないことを保証するために i : I という引数が必要です.これらの証明にあたっては, ext や intro を使って集合間の等式や包含関係を要素の式に展開し,次いで simp を使って要素の帰属についての条件を展開することをお勧めします.
variable {I : Type*} (A : I → Set α) (B : I → Set β)
example : (f '' ⋃ i, A i) = ⋃ i, f '' A i := by
sorry
example : (f '' ⋂ i, A i) ⊆ ⋂ i, f '' A i := by
sorry
example (i : I) (injf : Injective f) : (⋂ i, f '' A i) ⊆ f '' ⋂ i, A i := by
sorry
example : (f ⁻¹' ⋃ i, B i) = ⋃ i, f ⁻¹' B i := by
sorry
example : (f ⁻¹' ⋂ i, B i) = ⋂ i, f ⁻¹' B i := by
sorry
型理論では,関数 f : α → β は始域 α の任意の要素に適用することができますが,一部の要素にのみ意味のある関数を表現したいこともあります.例えば, ℝ → ℝ → ℝ 型の関数として,除算は第2引数が0でないときのみ意味を持ちます.数学をする上で, s / t という形の式を書く時は, t が0である場合を暗黙的または明示的に除外しているはずです.
しかし,Leanでは除算は ℝ → ℝ → ℝ 型を持つので第2引数が0のときにも値を返さなければなりません.このような問題に対してMathlibでは,関数の自然な定義域の外でも便宜的に値を与えるという戦略が一般的に取られています.例えば, x / 0 を 0 と定義すればすべての x , y , z に対して, (x + y) / z = x / z + y / z という等式が成り立ちます.
そのため,Leanで s / t という式を読むときに t が意味のある入力値であることを仮定すべきではありません.もしその仮定が必要である場合は,定理の仮定に制限を加えて,それが意味のある値であることを保証することができます.例えば,定理 div_mul_cancel は適切な代数構造の x と y に対して x ≠ 0 → x / y * y = x を保証するものです.
Mathlibでは f が s 上で単射であることを示す InjOn f s という述語が定義されています.これは以下のように定義されています:
example : InjOn f s ↔ ∀ x₁ ∈ s, ∀ x₂ ∈ s, f x₁ = f x₂ → x₁ = x₂ :=
Iff.refl _
Injective f は InjOn f univ に等価であることを証明することができます.同様にMathlibには {x | ∃y, f y = x} と定義される range f があり, range f と f '' univ が等しいことも証明可能です.このように関数の多くの特性は定義域全体に対して定義されますが,なかには定理の内容を定義域の部分集合に制限した相対化されたバージョンも存在します.これはMathlibでよく見られる方針です.
以下に InjOn と range の使用例を示します:
open Set Real
example : InjOn log { x | x > 0 } := by
intro x xpos y ypos
intro e
-- log x = log y
calc
x = exp (log x) := by rw [exp_log xpos]
_ = exp (log y) := by rw [e]
_ = y := by rw [exp_log ypos]
example : range exp = { y | y > 0 } := by
ext y; constructor
· rintro ⟨x, rfl⟩
apply exp_pos
intro ypos
use log y
rw [exp_log ypos]
以下を証明してみましょう:
example : InjOn sqrt { x | x ≥ 0 } := by
sorry
example : InjOn (fun x ↦ x ^ 2) { x : ℝ | x ≥ 0 } := by
sorry
example : sqrt '' { x | x ≥ 0 } = { y | y ≥ 0 } := by
sorry
example : (range fun x ↦ x ^ 2) = { y : ℝ | y ≥ 0 } := by
sorry
関数 f : α → β の逆関数を定義するにあたって,新しい概念を2つ用意しましょう.まず,Leanの型が空であるかもしれないという事実に対処する必要があります. f の逆関数を定義するにあたって,ある y に対して f x = y を満たすような x が無い場合, α 型のデフォルト値を割り当てたいところです.注釈 [Inhabited α] を variable として追加することは α 型がまさにこのような要素を持つことと同義であり,この要素は default と表記されます.次に, f x = y を満たすような x が複数存在する場合,逆関数はそのうちの1つだけを 選択 する必要があります.これには 選択公理 (axiom of choice)の力を借りる必要があります.Leanでは様々な方法で選択公理にアクセスすることができます.1つの便利な方法は,以下に示す古典論理に基づいた choose 関数を使用することです.
variable {α β : Type*} [Inhabited α]
#check (default : α)
variable (P : α → Prop) (h : ∃ x, P x)
#check Classical.choose h
example : P (Classical.choose h) :=
Classical.choose_spec h
h : ∃ x, P x が与えられた時, Classical.choose h の値は P x を満たすような x です.定理 Classical.choose_spec h は, Classical.choose h がこの仕様を満たすことを意味しています.
これらをもとに,以下のように逆関数を定義することができます:
noncomputable section
open Classical
def inverse (f : α → β) : β → α := fun y : β ↦
if h : ∃ x, f x = y then Classical.choose h else default
theorem inverse_spec {f : α → β} (y : β) (h : ∃ x, f x = y) : f (inverse f y) = y := by
rw [inverse, dif_pos h]
exact Classical.choose_spec h
noncomputable section と open Classical の行は古典論理を本質的な意味で使っているため必要です.入力 y に対して,関数 inverse f は f x = y を満たす x の値があればそれを返し,なければ α のデフォルトの要素を返します.これは 依存的なif (dependent if)による構成の例になっています.というのも条件が真の場合,返される値 Classical.choose h は仮定 h に依存するからです.条件式 if h : e then a else b は,等式 dif_pos h によって h : e が与えられると a に書き換えられ,同様に dif_neg h によって h : ¬ e が与えられると b に書き換えられます.また似たものとして if_pos と if_neg というものもあり,これは非依存なifの構成で機能し,これは次節で用いられます.定理 inverse_spec は inverse f が if 式の条件を満たすことを述べています.
これらがどのようにはたらくか完全に理解できなくても心配しないでください.定理 inverse_spec 単体で, f が単射であることと inverse f が f の左逆写像であることが同値であること, f が全射であることと inverse f が f の右逆写像であることが同値であることを示すことができます.vscodeで LeftInverse と RightInverse の定義をダブルクリックか右クリック,もしくは #print LeftInverse と #print RightInverse コマンドを使って調べてみてください.それから以下の2つの定理を証明してください.難しいですよ!細部を試行錯誤する前に,紙の上で証明することをお勧めします.それぞれの証明は6行程度で行えるはずです.更に挑戦したい場合は,それぞれの証明を1行の証明項に凝縮してみましょう.
variable (f : α → β)
open Function
example : Injective f ↔ LeftInverse (inverse f) f :=
sorry
example : Surjective f ↔ RightInverse (inverse f) f :=
sorry
本節を終えるにあたって,ある集合からその冪集合への全射が存在しないというカントールの有名な定理を型理論的に述べましょう.証明を理解した上で,欠けている2行を埋めてみてください.
theorem Cantor : ∀ f : α → Set α, ¬Surjective f := by
intro f surjf
let S := { i | i ∉ f i }
rcases surjf S with ⟨j, h⟩
have h₁ : j ∉ f j := by
intro h'
have : j ∉ f j := by rwa [h] at h'
contradiction
have h₂ : j ∈ S
sorry
have h₃ : j ∉ S
sorry
contradiction
4.3. シュレーダー=ベルンシュタインの定理
本章の最後として,集合論の初歩ですが自明ではない定理を述べましょう. \(\alpha\) と \(\beta\) を集合とします.(ここで行う形式化においては型とします) \(f : \alpha → \beta\) と \(g : \beta → \alpha\) がどちらも単射であると仮定します.直観的に, \(\alpha\) が \(\beta\) よりも大きくなく,また逆も同様であることを意味します.もし \(\alpha\) と \(\beta\) が有限集合である場合,これは両者が同じ濃度を持つことを意味します.19世紀,カントールは \(\alpha\) と \(\beta\) が無限の場合でも同じ結果が成り立つことを示しました.この事実はデデキント,シュレーダー,ベルンシュタインによってもそれぞれ独立に証明されています.
本節での形式化では後の章で詳しく説明する予定の新しい技法をいくつか導入します.ここでの説明が駆け足すぎると思われるかもしれませんが,心配しないでください.本節の目的は実際の数学的結果の形式的な証明に貢献するスキルを読者がすでに持っていることを示すことです.
この証明の背後にある考え方を理解するために, \(\alpha\) における写像 \(g\) の像を考えてみましょう.この像において, \(g\) の逆関数が定義され, \(\beta\) について全単射となります.
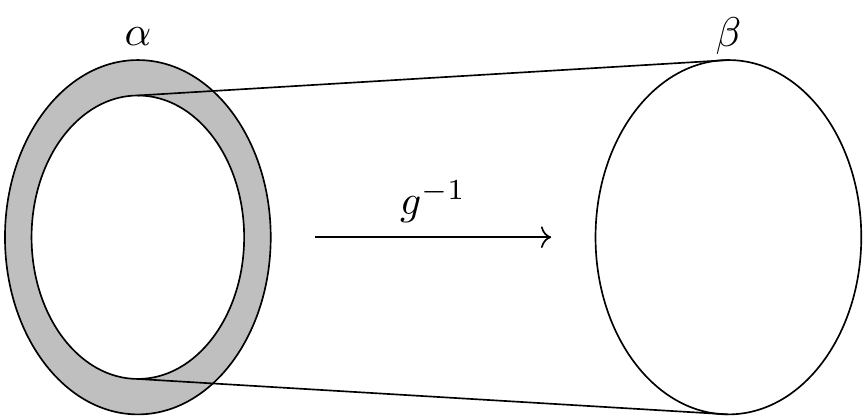
問題は, \(g\) が全射でない場合にはこの全単射が図中の斜線部分を含まないことです.これに対して \(f\) を使って \(\alpha\) の全要素を \(\beta\) に写すこともできますが,その場合 \(f\) が全射でなければ \(\beta\) の要素がいくつか漏れてしまうという問題があります.
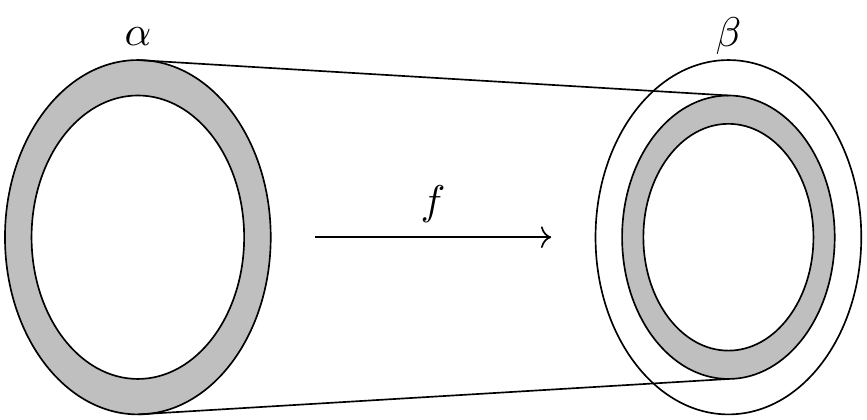
しかし,ここで \(\alpha\) からそれ自身への合成 \(g \circ f\) を考えてみましょう.この合成は単射となるため, \(\alpha\) とその像の間に全単射を構成し, \(\alpha\) の縮小されたコピーを \(\alpha\) 自身の中に生成します.
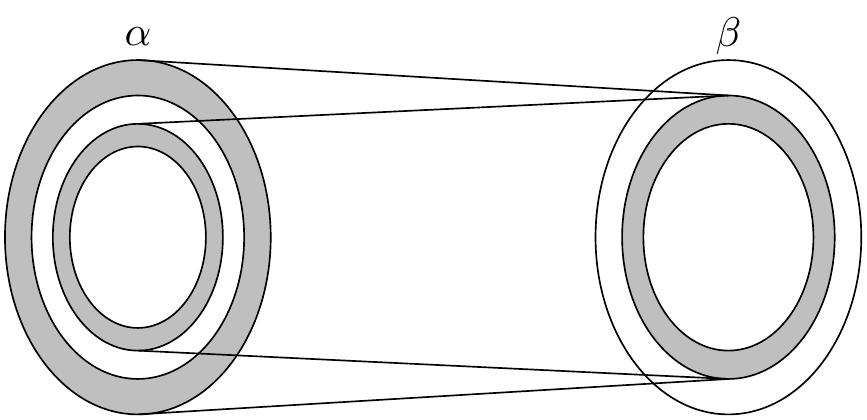
この合成は内側の斜線となっているリング [2] を,同心円状で小さくしたリングとしてさらにもう片方の集合の中に写し,この同心円的な構造が合成によって続いていきます.これによって斜線のリングによる同心円の列が形成されます.この列のそれぞれの斜線のリングは次のリングと全単射となっています.もし各リングを次のリングに対応させ, \(\alpha\) の斜線となっていない部分だけ残すと, \(\alpha\) と \(g\) のイメージの全単射が得られます.これを \(g^{-1}\) と合成すると,お望みの \(\alpha\) と \(\beta\) の間の全単射が得られます.
この全単射をもっと簡単に説明することもできます. \(A\) を一連の斜線領域の合併とし, \(h : \alpha \to \beta\) を以下のように定義します:
言い換えると,斜線部分には \(f\) を用い,それ以外には \(g\) の逆関数を使います.この結果得られる写像 \(h\) は単射となります.なぜなら \(h\) を構成している2つの関数はそれぞれ単射であり,この2つの像は互いに素であるためです.この関数が全射であることを確認するために, \(\beta\) の要素 \(y\) が与えられたと仮定し, \(g(y)\) を考えます.もし \(g(y)\) が斜線領域のどこかにいるならば,この斜線領域のリングの列の一番最初のリングにいることはありえないため,前のリングにある \(x\) に対して, \(g(y) = g(f(x))\) となります. \(g\) の単射性により, \(h(x) = f(x) = y\) が成り立ちます.もし \(g(y)\) が斜線領域に入っていなければ, \(h\) の定義により, \(h(g(y))= y\) となります.いずれにせよ \(y\) は \(h\) の像の中にいることになります.
この議論はもっともらしく聞こえることでしょうが,細部は微妙です.証明を形式化することは結果に対する信頼性を高めるだけでなく,よりよく理解するための助けにもなります.この証明では古典論理を使うため,本書の定義が一般には計算不可能であることをLeanに伝えます.
noncomputable section
open Classical
variable {α β : Type*} [Nonempty β]
注釈 [Nonempty β] は β が空でないことを示します.これは \(g^{-1}\) を構成するために使用するMathlibのプリミティブがこの前提を必要とするためです. \(\beta\) が空である場合,定理は自明になります.そのケースをカバーするために形式化を一般化することは難しくありませんが,ここでは省略します.具体的にはMathlibで定義されている演算 invFun を使うにあたって仮定 [Nonempty β] が必要になります. x : α が与えられた時, invFun g x は β に x の逆像があればそれを選び,なければ β の任意の要素を返します.関数 invFun g は g が単射であれば常に左逆であり, g が全射であれば常に右逆です.
#check (invFun g : α → β)
#check (leftInverse_invFun : Injective g → LeftInverse (invFun g) g)
#check (leftInverse_invFun : Injective g → ∀ y, invFun g (g y) = y)
#check (invFun_eq : (∃ y, g y = x) → g (invFun g x) = x)
斜線領域の合併に対応する集合を次のように定義します.
variable (f : α → β) (g : β → α)
def sbAux : ℕ → Set α
| 0 => univ \ g '' univ
| n + 1 => g '' (f '' sbAux n)
def sbSet :=
⋃ n, sbAux f g n
定義 sbAux は次章で説明する 再帰的定義(recursive definition) の一例です.これは以下の集合の列を定義します.
定義 sbSet は証明のスケッチで出てきた集合 \(A = \bigcup_{n \in \mathbb{N}} S_n\) に対応します.上述の関数 \(h\) は次のように定義されます:
def sbFun (x : α) : β :=
if x ∈ sbSet f g then f x else invFun g x
本節で定義した \(g^{-1}\) が \(A\) の補集合,つまり \(\alpha\) の斜線外の領域に対して右逆であるという事実が必要です.これは一番外側のリングである \(S_0\) が \(\alpha \setminus g(\beta)\) に等しいため, \(A\) の補集合は \(g(\beta)\) に含まれるからです.その結果 \(A\) の補集合に含まれるすべての \(x\) に対して, \(g(y) = x\) となる \(y\) が存在します.( \(g\) の単射性により,この \(y\) は一意ですが,次の定理では invFun g x は g y = x となる y のうちどれかを返すだけです.)
以下の証明を見て,大筋をつかめたら残りの部分を埋めてみてください.最後に invFun_eq を使う必要があります.ここで sbAux を使って書き直すと sbAux f g 0 が対応する定義している等式の右辺に置き換わることに注意しましょう.
theorem sb_right_inv {x : α} (hx : x ∉ sbSet f g) : g (invFun g x) = x := by
have : x ∈ g '' univ := by
contrapose! hx
rw [sbSet, mem_iUnion]
use 0
rw [sbAux, mem_diff]
sorry
have : ∃ y, g y = x := by
sorry
sorry
次に \(h\) が単射であることの証明に移りましょう.非形式的には証明は次のようになります.まず \(h(x_1) = h(x_2)\) とします.もし \(x_1\) が \(A\) の中にあれば, \(h(x_1) = f(x_1)\) であり, \(x_2\) が \(A\) の中にあることは以下のように示すことができます.仮に \(A\) の中にない場合, \(h(x_2) = g^{-1}(x_2)\) となります. \(f(x_1) = h(x_1) = h(x_2)\) より, \(g(f(x_1)) = x_2\) が成り立ちます. \(A\) の定義から, \(x_1\) は \(A\) の中にあるため \(x_2\) も \(A\) の中にあることになり,矛盾します.従って \(x_1\) が \(A\) にあれば, \(x_2\) も \(A\) にあり, \(f(x_1) = h(x_1) = h(x_2) = f(x_2)\) となります. \(f\) の単射性から \(x_1 = x_2\) が導かれます.上記の対称的な議論から \(x_2\) が \(A\) にあれば \(x_1\) も同様であることが示され, \(x_1 = x_2\) が導かれます.
残る可能性は \(x_1\) と \(x_2\) のどちらも \(A\) にないということだけです.この場合, \(g^{-1}(x_1) = h(x_1) = h(x_2) = g^{-1}(x_2)\) となります.両辺に \(g\) を適用することで \(x_1 = x_2\) となります.
もう一度,Leanでどのように議論が展開されるかを見るために,以下の証明を一行ごとに確認することをお勧めします. sb_right_inv を使って証明を終わらせることができるかも試してみてください.
theorem sb_injective (hf : Injective f) : Injective (sbFun f g) := by
set A := sbSet f g with A_def
set h := sbFun f g with h_def
intro x₁ x₂
intro (hxeq : h x₁ = h x₂)
show x₁ = x₂
simp only [h_def, sbFun, ← A_def] at hxeq
by_cases xA : x₁ ∈ A ∨ x₂ ∈ A
· wlog x₁A : x₁ ∈ A generalizing x₁ x₂ hxeq xA
· symm
apply this hxeq.symm xA.symm (xA.resolve_left x₁A)
have x₂A : x₂ ∈ A := by
apply _root_.not_imp_self.mp
intro (x₂nA : x₂ ∉ A)
rw [if_pos x₁A, if_neg x₂nA] at hxeq
rw [A_def, sbSet, mem_iUnion] at x₁A
have x₂eq : x₂ = g (f x₁) := by
sorry
rcases x₁A with ⟨n, hn⟩
rw [A_def, sbSet, mem_iUnion]
use n + 1
simp [sbAux]
exact ⟨x₁, hn, x₂eq.symm⟩
sorry
push_neg at xA
sorry
この証明ではいくつか新しいタクティクを導入しています.まず set タクティクに注目します.これは sbSet f g と sb_fun f g に対してそれぞれ A と h という略語を導入するものです.またこの対応を定義する等式に A_def と h_def と名付けています.この省略は定義的なものであり,Leanは必要に応じて自動的に省略形を展開することがあります.しかし常に行われるわけではありません.例えば, rw を使用する場合,一般的には A_def と h_def を明示的に使用する必要があります.つまり,定義はトレードオフの関係にあるのです.式をより短く読みやすくすることができますが,時にはより多くの作業が必要に成ります.
より興味深いタクティクは wlog タクティクで,これは上記の非形式的な証明における対称性の議論をカプセル化したものです.このタクティクについては今触れませんが,このタクティクはまさに望みの挙動を実現しています.このタクティクにカーソルを合わせるとドキュメントを見ることができます.
全射の議論はもっと簡単です. \(y\) が \(\beta\) にあるとすると, \(g(y)\) が \(A\) にあるかどうかによって2つのケースが考えられます.もし \(A\) にある場合,定義上 \(g\) の像とは素であるため,一番外側のリングである \(S_0\) には入りえません.従って,これはある \(n\) の \(S_{n+1}\) の要素となります.これは \(S_n\) の要素 \(x\) に対して \(g(f(x))\) の形であることを意味します. \(g\) の単射性から \(f(x) = y\) が成り立ちます. \(g(y)\) が \(A\) の補集合にある場合, \(h(g(y))= y\) が直ちに得られるため,これで証明が完了します.
ここでもまた,以下の証明を見て欠けている部分を埋めてみましょう.タクティク rcases n with _ | n は g y ∈ sbAux f g 0 と g y ∈ sbAux f g (n + 1) の2つの場合に分かれます.どちらの場合も, simp [sbAux] で単純化すると, sbAux の対応する定義の等式が適用されます.
theorem sb_surjective (hg : Injective g) : Surjective (sbFun f g) := by
set A := sbSet f g with A_def
set h := sbFun f g with h_def
intro y
by_cases gyA : g y ∈ A
· rw [A_def, sbSet, mem_iUnion] at gyA
rcases gyA with ⟨n, hn⟩
rcases n with _ | n
· simp [sbAux] at hn
simp [sbAux] at hn
rcases hn with ⟨x, xmem, hx⟩
use x
have : x ∈ A := by
rw [A_def, sbSet, mem_iUnion]
exact ⟨n, xmem⟩
simp only [h_def, sbFun, if_pos this]
exact hg hx
sorry
これですべてをまとめることができます.この証明は Bijective h が Injective h ∧ Surjective h に展開されることを利用しているため,短く,そして美しいものになっています.
theorem schroeder_bernstein {f : α → β} {g : β → α} (hf : Injective f) (hg : Injective g) :
∃ h : α → β, Bijective h :=
⟨sbFun f g, sb_injective f g hf, sb_surjective f g hg⟩
訳注: 本節中で「リング」と書いている箇所はすべて説明に用いられた図中の集合内にある斜線等で表現された輪を指し,代数構造の環のことを指しません.